|
Step by Step Instructions |
|||
| Evaluate Functions | 1. Replace the independent variable, x, with place holders. 2. Insert value or variable or function in the placeholder. 3. Complete the algebraic evaluation. eg: G: f(x) = 3x - 1 F: f(2), f(a+1) f( ) = 3 ( ) -1 f(2) = 3(2) - 1 = 5 f(a+1) = 3(a+1) - 1 = 3a + 3 - 1 = 3a +2 |
||
| Solving Rational Eq. | 1. Find LCD (factor if necessary) 2. Is check required? MUST check if LCD contains a variable. 3. Use Multiplication Property of Equality to multiply all terms by the LCD. 4. Simplify using distributive property or combining like terms, etc. 5. Solve the equation. 6. Check if MUST. If checks correctly, then step 5 solution is the answer. If does not check correctly, then there is no solution. |
||
Sketching Polynomials
|
1. Determine degree n, and leading cooeficient, an of
the polynomial 2. Overview sketch: a) end behavior, b) max # zeros, c) max # extrema 3. Find zeros. 4. Set up table of intervals using the zeros as endpoints and selecting convenient values of x within the intervals. 5. Find the corresponding y values or each x selected above, and enter the y value and the ordered pair (x,y) into the table. 6. Plot the known points, including the zeros. 7. Use your overview, together with the plotted points to complete an estimated sketch. Note that we do not know the exact locations of extrema, only approximations. |
||
|
Synthetic Division P(x)
|
1. Determine c. |
||
|
Exact Values of Trig Functions of Special Angles
|
1. Sketch the x-y coordinate system. 2. Draw the given angle. a) Use the quadrantal angles as reference: π / 2 = 90° π = 180° 3π / 2 = 270° 2π = 360° b) Determine the location of the terminal ray. 3. Drop a perpendicular to form the right triange. 4. Label the sides and hypotenuse. a) For the magnitude, use measures associated with the special triangle. in degrees: sin 30° = 1/2 tan 45° = 1 in radians: sin π/6 = 1/2 tan π/4 = 1 b) For each side use the sign appropriate for the quadrant. The radius is always positive. 5. Determine the trig function, using the appropriate ratio of definition. |
||

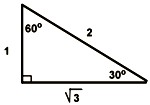
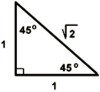 45°=π / 4
45°=π / 4